경사 하강법(Gradient Descent)
Gradient Descent, SGD, Batch
안녕하세요. 데이터 사이언티스트를 위한 정보를 공유하고 있습니다.
M1 Macbook Air를 사용하고 있으며, 블로그의 모든 글은 Mac을 기준으로 작성된 점 참고해주세요.
경사 하강법(Gradient Descent)
회귀를 통한 설명이 경사 하강법을 직관적으로 이해하는 데 더 수월하기 때문에
이전 포스팅의 회귀와 이어서 설명하도록 하겠습니다.
회귀는 데이터를 반복적으로 학습하면서, 즉 w(weight: 가중치)와 b(bias: 편향)를 반복적으로 업데이트 하면서
비용 함수가 최소가 되도록 하는 파라미터(w, b)를 구하는 것이 목적이라고 하였습니다.
이때 최적의 파라미터를 찾아내는 과정의 알고리즘을 옵티마이저(Optimizer)라고 부르고,
그중 기본적이며 대표적인 옵티마이저 알고리즘이 바로 경사 하강법입니다.
비용 함수의 최솟값을 찾기 위해 기울기를 활용하는 방식이며
인공신경망 기반의 딥러닝을 비롯한 머신러닝에서는 아주 중요한 개념입니다.
경사 하강법의 이해를 돕기 위해 비용 함수를 간단히 w에 대한 2차 함수 곡선의 형태로 나타내면 다음 그림과 같을 것입니다.
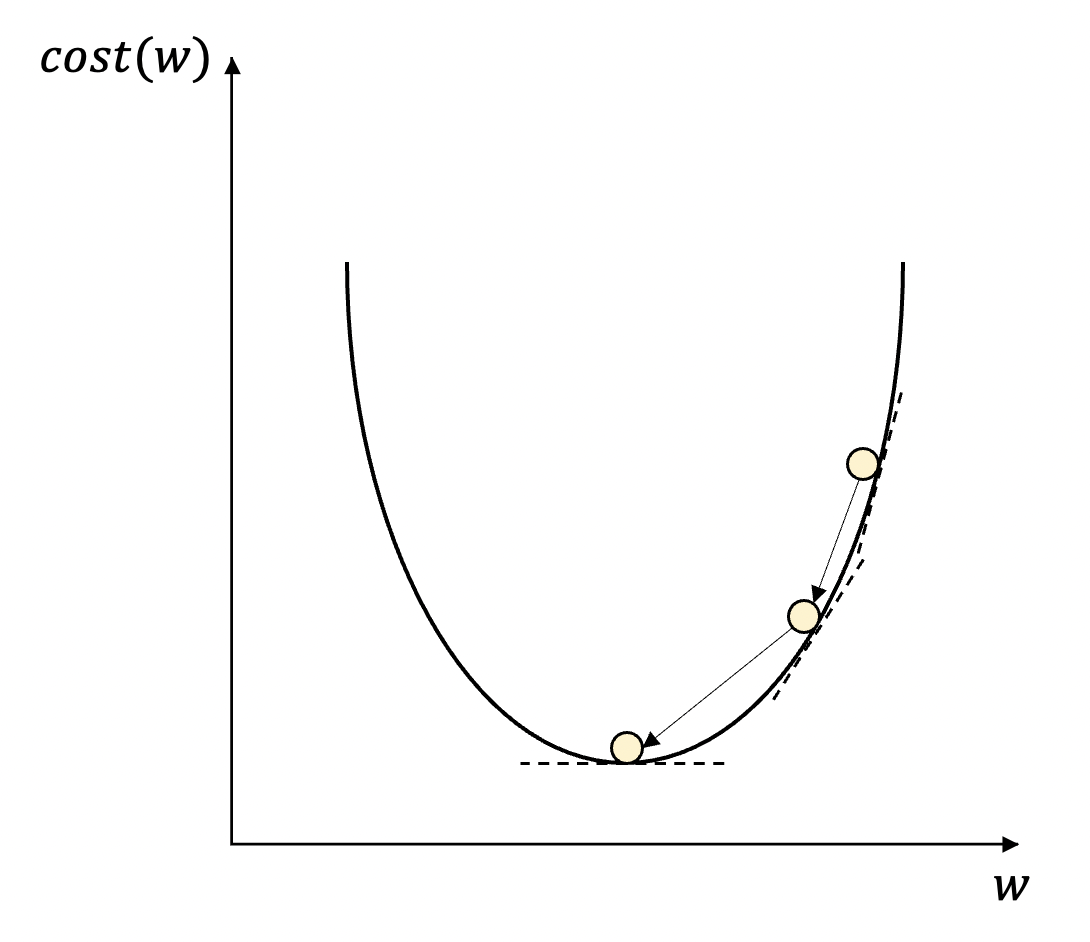
이때 처음 위치에서 기울어진 방향으로 학습을 반복하여 오류를 줄여나가며 최소 지점을 찾아내는 것이 경사 하강법입니다.
물론 기울기가 0이 되는 지점이 반드시 최솟값을 나타내진 않습니다.
그림과 달리 비용 함수는 대체로 훨씬 복잡한 형태를 띄고 있으며
따라서 극솟값(기울기가 0인 지점)은 실제로 여러 개 존재할 것입니다.
다만 이번 포스팅에서는 경사 하강법이 어떤 방식으로 진행되는지만 기억해주시길 바랍니다.
이번에는 수식을 통해 살펴보겠습니다.
머신러닝과 딥러닝에서 분류, 회귀 등 다양한 문제가 있고 각각의 문제에 적합한 비용 함수가 따로 있습니다.
통칭해서 비용 함수를 cost(w)라고 하겠습니다.
이때 w가 업데이트 되는 방식은 다음과 같습니다.
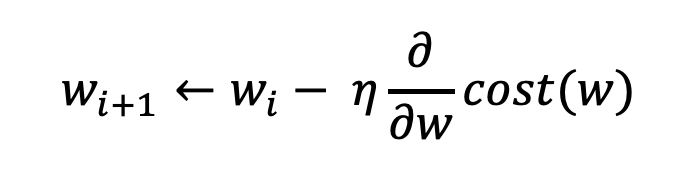
비용 함수의 접선의 기울기에 η(learning rate: 학습률)를 곱한 값을
기존의 w에서 빼준 값이 새로운 w가 됩니다.
접선의 기울기는 w의 위치에 따라 음수일 수도 양수일 수도 있습니다.
하지만 어느 경우든 위의 방식대로 계산된다면 w는 항상 기울기가 0인 방향으로 업데이트 됩니다.
이때 편미분 된 값이 너무 클 수 있기 때문에 이를 보정하기 위한 보정 계수가 바로 학습률 η 입니다.
w가 새로 학습(업데이트)될 때마다 얼마나 크게 변경될 것인지 결정하는,
즉 그림으로 보면 w가 얼마나 큰 폭으로 움직일지 결정하는 값이며,
일반적으로 0과 1사이의 값으로 설정합니다.
학습률이 너무 큰 경우에는 다음 그림과 같이 발산하여 오히려 최소점에서 멀어지는 현상(overshooting)이 발생합니다.
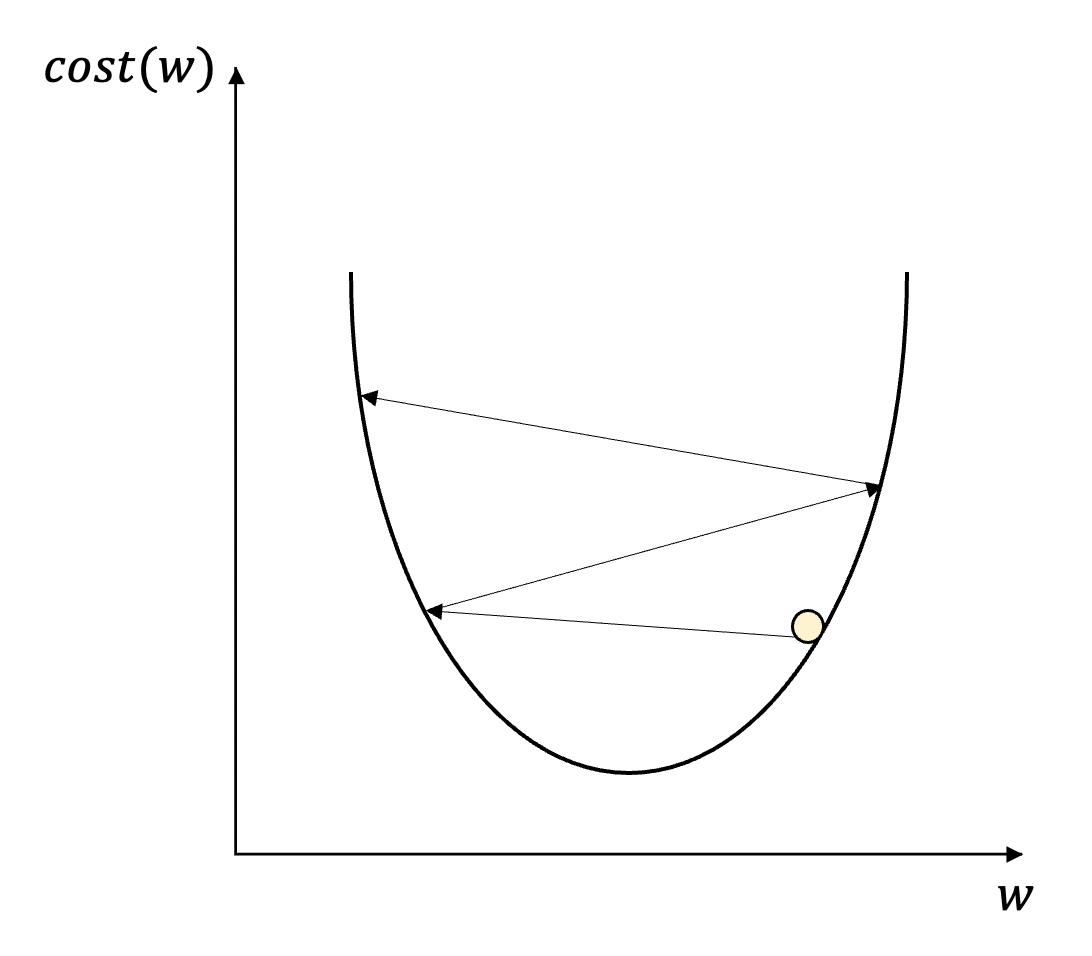
반대로 너무 작은 경우에는 그만큼 학습 시간이 지나치게 오래 걸리게 됩니다.
따라서 학습률은 충분히 작게, 하지만 지나치게 작지는 않게 적당한 값으로 설정해주어야 합니다.
또한 실제로 비용 함수는 복잡하여 w0, w1, w2, … 등 변수가 더 다양할 수 있으며
이때의 기울기 값은 각 w에 대하여 편미분하여 계산합니다.
실제 경사하강법에서는 w과 b가 모두 업데이트 된다는 것을 기억해주시길 바랍니다.
SGD(Stochastic Gradient Descent: 확률적 경사 하강법) vs Mini-Batch GD
일반적인 경사 하강법은 학습을 진행할 때
모든 데이터 샘플마다 각각 파라미터를 업데이트하므로 시간이 매우 오래 걸린다는 단점이 있습니다.
또한 딥러닝의 경우에는 레이어가 많으면 메모리 부족으로 연산이 불가능할 수도 있습니다.
이를 해결하기 위해 전체 데이터 중에서 임의로 한 건만 선택하여 경사 하강법을 실시하는데
이러한 방식이 바로 SGD 알고리즘입니다.
고작 데이터 한 건으로 경사 하강법을 진행하면 과연 신뢰할만 할까?
그래서 Mini-Batch GD 알고리즘이 있습니다.
여기서 배치(batch)는 한국어로 집단, 뭉텅이을 의미하는데
학술적으로는 전체 데이터 중에서 임의로 특정 배치 사이즈 만큼 선택하여 경사 하강법을 실시하는 방법입니다.
하지만 프레임워크에서 어떻게 다루어지는지가 중요하겠죠.
일반적인 딥러닝 프레임워크에서는 SGD가 곧 SGD with Mini-Batch인데,
지정한 배치 사이즈에 따라 전체 데이터를 여러 개의 배치로 나누고
배치마다 오류값을 모두 합산하여 배치 별로 한 번에 파라미터를 업데이트하는 방식으로 진행됩니다.
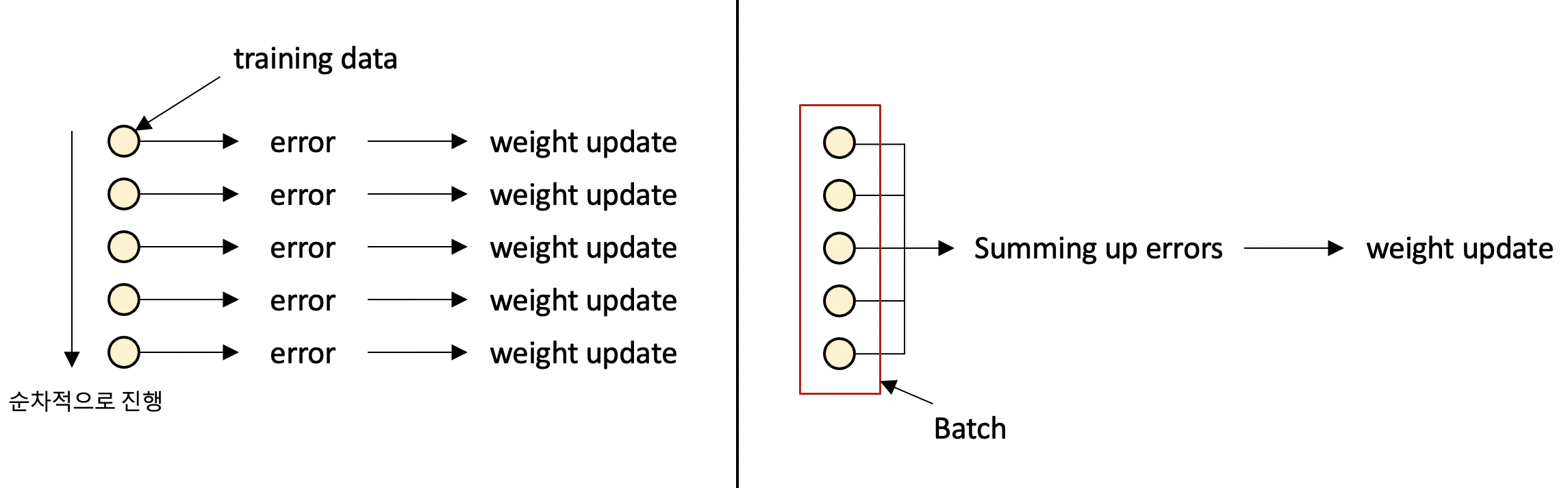
왼쪽 그림은 각각의 데이터 샘플 별로 오류를 계산하고, 파라미터를 업데이트하는 방식을 나타낸 것이고(Online algorithm),
오른쪽 그림은 일반적인 딥러닝 프레임워크에서 동작하는 Mini-Batch GD 방식을 나타낸 것입니다(Batch algorithm).
예를 들어 데이터의 샘플 수가 10,000개면,
전자의 경우에는 각 데이터 샘플 별로 학습이 진행되어 w 업데이트가 10,000번 진행되고,
후자의 경우에는 배치 사이즈를 100으로 지정했을 때, 각 배치 별로 한 번씩, 즉 w 업데이트가 100번만 진행되는 것입니다.
읽어주셔서 감사합니다.
정보 공유의 목적으로 만들어진 블로그입니다.
미흡한 점은 언제든 댓글로 지적해주시면 감사하겠습니다.
댓글남기기